SHA256_Transform() 함수의 알고리즘에 대해서 이전 포스팅에서 분석하였다.
이번에는 FIPS-180 문서를 통해 더욱 자세히 분석해보려 한다.
먼저 알아둘 것이 있다면 for문을 제외하고는 알고리즘 모양이 같다.
0. 기호
SHA-256 해시 계산 알고리즘에서 사용될 함수 및 수식에 대해서 정의하고 시작하겠다.
ROTR: rotate right shift
SHR: right shift
$Ch\left ( x,y,z \right ) = \left ( x\wedge y \right )\oplus \left ( \bar{x}\wedge z \right )$
$Maj\left ( x,y,z \right ) = \left ( x\wedge y \right )\oplus \left ( x\wedge z \right )\oplus \left ( y\wedge z \right )$
$\sum_{0}\left( x \right )=ROTR^{2}\left ( x \right )\oplus ROTR^{13}\left ( x \right )$
$\sum_{1}\left( x \right )=ROTR^{6}\left ( x \right )\oplus ROTR^{11}\left ( x \right )$
$\sigma_{0}\left( x \right )=ROTR^{7}\left ( x \right )\oplus ROTR^{18}\left ( x \right )\oplus SHR^{3}\left ( x \right )$
$\sigma_{1}\left( x \right )=ROTR^{17}\left ( x \right )\oplus ROTR^{19}\left ( x \right )\oplus SHR^{10}\left ( x \right )$
1. 해시 계산 알고리즘(Hash Computation Algorithm)
1.1. 상수 W
상수 W(t) : 64개의 배열로 이루어진다.
- 0≤ t ≤ 15
: 메시지 배열 0~15번을 그대로 가져다 사용 - 16 ≤ t ≤ 63
: 다음과 같은 수식을 사용
$\sigma _{1}\left ( W_{t-2}\right)+W_{t-7}+\sigma _{0}\left ( W_{t-15}\right)+W_{t-16}$
1.2. 초기 해시값 대입
a, b, c, d, e, f, g, h에 첫 번째 해시값부터 마지막 해시값을 넣는다.
$a=H_{0}$
$a=H_{1}$
...
1.3. For t=0 to 63
$T_{1}=h+\sum_{1}\left( e \right )+Ch\left ( e,f,g \right )+K^{256}_{t}+W_{t}$
$T_{2}=\sum_{0}\left( a \right )+Maj\left ( a,b,c \right )$
$h=g$
$g=f$
$f=e$
$e=d+T_{1}$
$d=c$
$c=b$
$b=a$
$a=T_{1}+T_{2}$
위의 식을 쉽게 이해해보자!
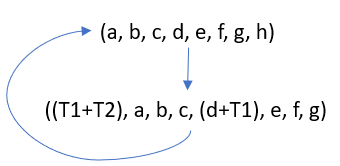
t를 0부터 63까지 1씩 증가시키는 반복문이다.
만약 t=0일 때 (a, b, c, d, e, f, g, h)이 계산된다면 아래와 같은 값을 가지게 된다.
a = $T_{1}+T_{2}$
b = a
c= b
d= c
e = $d+T_{1}$
f = e
g = f
h = g
rotate shift right의 형태를 가지게 되어
t=1일 때는 a가 있던 자리에는 T1+T2가 들어오고,
e가 있던 자리에는 d+T1가 들어온다.
1.4. 최종 해시값 계산
해시값 8개를 각각 a부터 h까지 더한다.
$H_{0}=a+H_{0}$
$H_{1}=b+H_{1}$
$H_{2}=c+H_{2}$
...
계산을 마친 $H_{0}$부터 $H_{7}$까지를 붙여서 최종 해시값을 만든다.
- 출처 -
'Security > SHA' 카테고리의 다른 글
| [SHA-256] 코드 실행 및 해시값 비교 방법 (0) | 2021.07.17 |
|---|---|
| [SHA-256] 코드 및 알고리즘 분석 - (4) (0) | 2021.07.14 |
| [SHA-256] 코드 및 알고리즘 분석 - (3) (0) | 2021.07.14 |
| [SHA-256] 코드 및 알고리즘 분석 - (2) (0) | 2021.07.13 |
| [SHA-256] 코드 및 알고리즘 분석 - (1) (0) | 2021.07.12 |
![[SHA-256] 코드 및 알고리즘 분석 - (5)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FJzCUA%2Fbtq9I0ZaeyI%2FVd19X75toweR3GgIYWLkyK%2Fimg.png)